AAC1 P5 - Odd Alpacas

Problem Link: dmoj.ca/problem/aac1p5

This post will discuss the solution for the problem linked above. I created this problem along with Sam Liu for Animal Contest 1 on DMOJ.

Statistics:

• Served as P5 of a 6-problem set.
• ~9~ correct submissions during contest.
• ~29.33\%~ AC rate (including subtasks).

Statement

You are given an tree of ~N~ nodes and ~N - 1~ weighted edges connecting ~u_i~ and ~v_i~ with weight ~w_i~ for ~1 \le i \le N - 1~.

Let the “length” of a path ~(x, y)~ to be the sum of weights on the edges from node ~x~ to node ~y~.

Let ~x~ to be the number of even length paths, and ~y~ to be the number of odd length paths.

By changing the weight of one edge, minimize ~|x - y|~.

Note: You are allowed to modify ~0~ edges.

Subtask 1

The constraint ~1 \le N \le 200~ was set on purpose to allow brute force solutions to pass for ~10\%~ of points.

First, notice how the modification of an edge modifies a path length.

Suppose a path was defined of the following weight parities:

The parity of ~\text{len}~ would only change if one of the 4 parities also changed. This is either changing an ~\text{odd}~ to an ~\text{even}~ or the other way around.

Hence, for this subtask we can simulate changing the parity for each edge. Once that is done, how can we find ~x~ and ~y~?

For each node ~v~ ~(1 \le v \le N)~, run a dfs on an assumption that ~v~ is an endpoint on a path. Create a distance array maintaining parity and ~|x - y|~ can be found easily.

Time Complexity: ~\mathcal{O}(N^3)~

Code Snippets

void Dfs(int v, int pr) { 
  for (const auto p : g[v]) { 
    int to = p.first;
    int w = p.second;
    if (to == pr) {
      continue;
    }
    if (min(to, v) == mod_x && max(to, v) == mod_y) {
      w ^= 1;
    }
    dist[to] = dist[v] + w;
    Dfs(to, v);
  }
};

if mod_x and mod_y are the nodes we are modifying, we can do a check and do w ^= 1 to switch the parity.

int x = get<0>(e);
int y = get<1>(e);
if (x > y) {
  swap(x, y);
}     
mod_x = x;
mod_y = y;
{
  long long odd = 0;
  long long even = 0; 
  for (int i = 0; i < n; i++) {
    dist.assign(n, 0);
    Dfs(i, -1);
    for (int j = 0; j < n; j++) {
      if (i == j) { 
        continue;
      }
      odd += (dist[j] % 2 == 1);
      even += (dist[j] % 2 == 0);
    }
  }
  odd /= 2;
  even /= 2;  
  ans = min(ans, abs(odd - even));
}

For each edge ~(x, y)~, we can set these as mod_x and mod_y and run a dfs for each node from ~1~ to ~N~.

Note: This implementation uses 0-based indexing. Hence the nodes are labeled from ~0~ to ~N - 1~.

Subtask 2

Constraints in this subtask (~1 \le N \le 2 \times 10^3~) were set to allow for a more optimized brute force to pass.

If ~N = 2 \times 10^3~, a ~\mathcal{O}(N^2)~ algorithm with about ~4 \times 10^6~ operations will pass.

We can draw inspiration from a very common ~\text{LCA}~ property used to find distance between two nodes in a tree:

If ~\text{dist}[x]~ is the distance from the root (~1~):

Notice that any number (odd or even), when multipled by ~2~ will always result in a ~even~ result. Since ~ 2 \times \text{dist}[\text{lca}(x, y)]~ will always be even, the parity of ~\text{dist}(x, y)~ will be determined by ~\text{dist}[x]~ and ~\text{dist}[y]~.

So:

• If ~\text{dist}[x] + \text{dist}[y]~ is odd, ~\text{dist}(x, y)~ will be odd.
• If ~\text{dist}[x] + \text{dist}[y]~ is even, ~\text{dist}(x, y)~ will be even.

Let ~\alpha = \text{dist}[x] + \text{dist}[y]~.

Now, we want to be able to count ~x~ and ~y~ in ~\mathcal{O}(N)~ time, since we are trying each ~N - 1~ edges.

To count all paths with ~\alpha \equiv 1 \pmod 2~, we can multiply the number of nodes ~v~ with odd distance by the number of nodes with even distance. Let this result be ~\text{odd}~.

For the other case ~\alpha \equiv 0 \pmod 2~, we can subtract the number of odd paths from the total number of paths: (~\frac{n \cdot (n - 1)}{2} - \text{odd}~).

Time Complexity: ~\mathcal{O}(N^2)~

Code Snippets

long long odd = 0;
long long even = 0;
for (int i = 0; i < n; i++) {
  odd += (dist[i] % 2 == 1);
  even += (dist[i] % 2 == 0);
}     
long long o_cnt = odd * even;
long long e_cnt = n * (n - 1) / 2 - o_cnt;  
ans = min(ans, abs(o_cnt - e_cnt));

For each edge ~i~ (~1 \le i \le N - 1~), we run a DFS and calculate ~|x - y|~ like so.

Subtask 3

For the final subtask with ~(1 \le N \le 2 \times 10^5)~, a ~\mathcal{O}(N)~ algorithm must be derived.

The intended solution still goes on the assumption that all edges must be tried, but has an constant time way of finding ~x~ and ~y~.

Define an “odd” node to be an arbitrary node ~v~ such that ~\text{dist}[v] \equiv 1 \pmod 2~.

Define an “even” node to be an arbitrary node ~v~ such that ~\text{dist}[v] \equiv 0 \pmod 2~.

Suppose an edge ~(x, y)~ parity is changed. What paths are affected by this edge?

We can make the claim that:

• Any path ~(u, v)~ intersecting edge ~(x, y)~ will have either ~u~ or ~v~ in the subtree of edge ~(x, y)~.

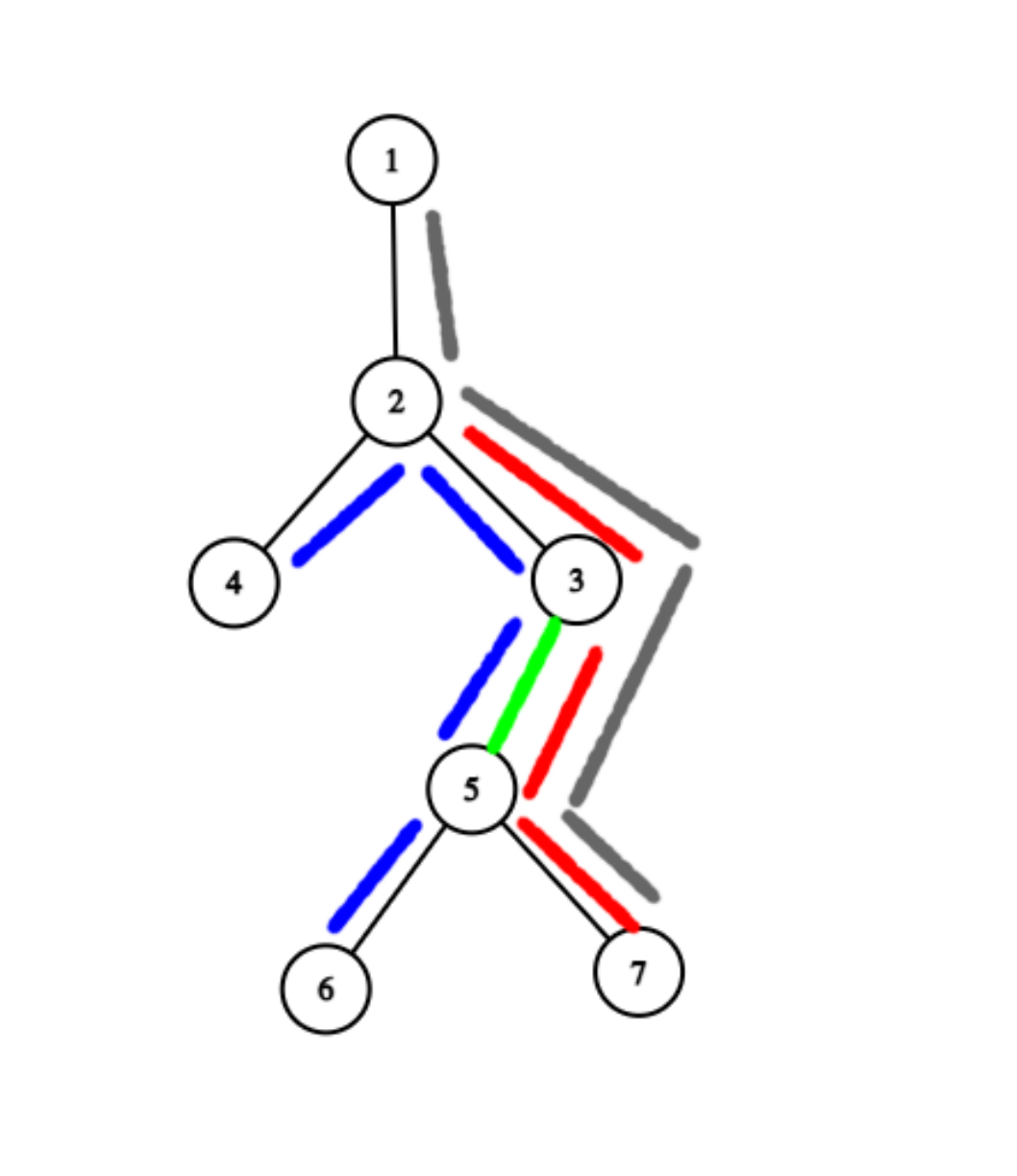
Take the tree above, if the edge ~(3, 5)~ (highlighted in green) was modified, notice that the grey, red, and blue path all have a end-vertex in the subtree of ~(3, 5)~.

We can notice that all even nodes will swap to odd nodes and vise-versa in this subtree, because all paths must have an end-point in the subtree.

Hence, if we keep a counter for the number of odd and even nodes in each subtree, when the time comes to modify an edge ~(x, y)~ we can swap the odd and even nodes appropriately and calculate ~x~ and ~y~ with the formula described in Subtask 2.

Time Complexity: ~\mathcal{O}(N)~

Code Snippets

long long ov = 0, ev = 0;
for (int i = 0; i < n; i++) {
  ov += (d[i] % 2 == 1);
  ev += (d[i] % 2 == 0);
}
long long o_cnt = ov * ev;
long long e_cnt = n * (n - 1) / 2 - o_cnt;
long long ans = abs(o_cnt - e_cnt); 
for (const auto& e : es) {
  int x, y, z;
  tie(x, y, z) = e;
  if (dep[x] < dep[y]) {
    swap(x, y);
  }
  long long o_aux = ov - odd[x] + even[x];
  long long e_aux = ev - even[x] + odd[x];
  long long new_o_cnt = o_aux * e_aux;
  long long new_e_cnt = n * (n - 1) / 2 - new_o_cnt;
  ans = min(ans, abs(new_o_cnt - new_e_cnt));
}
cout << ans << '\n';